An Encryption that Remains Dangerous even When Used Just Once?
Overcoming the Limitations of GCM

– Proposal by Samsung SDS

What is GCM Authenticated Encryption scheme, and what is Samsung SDS's Approach?

The GCM authenticated encryption (AE) scheme, one of the most widely used AE schemes in the world, while it suffers from risk of nonce misuse, short message length per encryption, and insufficient level of security. The goal of this paper is to design new AE schemes achieving stronger provable security in the standard model and accepting longer nonces (or providing nonce misuse resistance), with the design rationale behind GCM.

As a result, we propose two enhanced variants of GCM and GCM-SIV, dubbed eGCM and eGCM-SIV, respectively. eGCM and eGCM-SIV are built on top of a new CENC-type encryption mode, dubbed eCTR: using 2n-bit counters, eCTR enjoys beyond-birthday-bound security without significant loss of efficiency. eCTR is combined with an almost uniform and almost universal hash function, yielding a variable input-length variable output-length pseudorandom function, dubbed HteC. GCM and GCM-SIV are constructed using eCTR and HteC as building blocks.

eGCM and eGCM-SIV accept nonces of arbitrary length, and provide almost the full security (namely, n-bit security when they are based on an n-bit block cipher) for a constant maximum input length, under the assumption that the underlying block cipher is a pseudorandom permutation (PRP). Their efficiency is also comparable to GCM in terms of the rate and overall speed.

* Birthday Bound: Intuitively, it refers to the phenomenon where collisions occur with fewer people than expected. In cryptography, the birthday bound represents security limitations that arise when using n-bit block ciphers or hash functions.

Samsung SDS's Core Research Keywords: eCTR, HteC, eGCM, eGCM-SIV

• eCTR(enhanced Counter Mode): Propose an advanced counter mode that surpasses the birthday bound ($O(2^{n/2})$) of traditional CR mode, achieving nearly full n-bit –security ($O(2^n)$).
• HteC(Hash-then-eCTR): A variable input length-variable output length (VIL-VOL) pseudorandom function (PRF) built on eCTR, delivering a new (almost) full security.
• eGCM(enhanced GCM): An improved version of GCM that integrates eCTR and HteC, offering support for arbitrary-length nonces and enhanced security bounds.
• eGCM-SIV: An improved variant of GCM-SIV that retains nonce misuse resistance while enabling arbitrary-length nonces and providing improved security bounds.

Tweakable Enciphering Schemes Based on eCTR

In this paper, we propose a tweakable Enciphering Schemes(TES) based on eCTR.

• Concept of Tweakable Enciphering: This approach introduces an additional parameter (tweak) into encryption process to enhance flexibility and security.
• Areas of Applications: The proposed tweakable enciphering schemes can be applied to various areas, including disk encryption and database encryption.

eCTR: CTR-type Mode of Operation with Full Security [Theorem 1]

In this section, we propose a eCTR (enhanced Counter Mode), a new cipher-based encryption mode that overcomes the limitations of the traditional CTR mode. While the traditional CTR mode is constrained by the birthday bound (O(2^(n/2))), eCTR provides almost optimal n-bit security (O(2^n)).

The key features of eCTR are as follows:

• It significantly reduces the probability of internal state collisions using a 2n-bit counter
• It maintains efficiency by minimizing the number of block cipher calls.
• It guarantees ease of implementation by retaining a structure similar to the traditional CTR mode.

The operation of eCTR proceeds as follows:

• Set an initial counter value.
• Increment the counter value for each block encryption.
• Encrypt the counter value using block cipher and XOR the result with plaintext to generate ciphertext.

In this section, we present a formal definition of eCTR along with theoretical justifications for how it overcomes the birthday bound of traditional CTR mode. Additionally, we provide formal security claims for eCTR in Theorem 1.

Proof of [Theorem 1]

In this section, we provide a formal proof of Theorem 1 regarding the security of eCTR. The proof is structured into the following key steps:

• Application of the Coefficient-H technique: Analyzes distinguishability between an ideal random function and the eCTR implementation.
• Analysis of Bad Transcripts: Identifies scenarios where a distinguisher can differentiate between the ideal world and the real world.
• Calculation of Collision Probability: Demonstrates how the probability of internal state collisions decreases by using a 2n-bit counter.
• Application of Mirror Theory: Applies mirror theory to analyze the probability of internal state collisions.
• Derivation of the Final Security Bound: Synthesizes the analysis results to prove that eCTR provides nearly optimal n-bit security.

Through this proof, we mathematically demonstrate that eCTR overcomes the birthday bound of traditional CTR mode and provides almost full n-bit security.

HteC: An Almost Optimally Secure VIL-VOL PRF [Theorem 2]

In this section, we introduce HteC (Hash-then-eCTR), a variable input length-variable output length (VIL-VOL) pseudorandom function based on eCTR. HteC is composed of the following two main components:

• Almost uniform and almost universal hash function (AXU hash): Converts inputs of arbitrary length into fixed-length hash value.
• eCTR: Utilizes the hash value to generate outputs of the desired length.

The operation of HteC proceeds as follows:

• Hash the input message using the AXU hash function.
• Use the hash value as the initial counter value for eCTR.
• Use eCTR to generate outputs of the desired length.

In this section, we present formal definition of HteC, accompanied by theoretical justifications that demonstrate its ability to achieve nearly optimal security. Additionally, we provide a formal security claim about HteC in Theorem 2.

Proof of [Theorem 2]

In this section, we provide a formal proof of Theorem 2 regarding the security of HteC. The proof is structured as follows:

• Analysis of HteC's Structure: Analyzes how HteC combines AXU hash function and eCTR.
• Utilization of AXU Hash Function Properties: Examines how the properties of almost uniform and almost universal hash function contribute to security.
• Utilization of eCTR's Security: Analyzes how the security of eCTR, proven in Theorem 1, contributes to the security of HteC.
• Application of Hybrid Argument: Applies a hybrid argument to analyze difference between an ideal hash function and an actual hash function.
• Derivation of Final Security Bound: Synthesize the analysis results to prove that HteC achieves optimal security.

Through the proof, we mathematically demonstrate that HteC achieves near-optimal security as a variable input length-variable output length pseudorandom function. This serves as a critical foundation for the security of eGCM and eGCM-SIV.
The eCTR and HteC presented in this section are key building blocks of the main contributions of this paper, namely eGCM and eGCM-SIV. In subsequent section, we explain how eGCM and eGCM-SIV are constructed based on these two components.

eGCM Authenticated Encryption Scheme: Efficient Encryption GCM’s Limitations

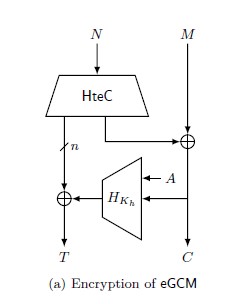
In this section, we propose eGCM (enhanced GCM), an improved variant of the existing GCM (Galois/Counter Mode). eGCM is constructed based on the previously described eCTR and HteC, overcoming several limitations of GCM while maintaining its design philosophy and efficiency.

The key features of eGCM are as follows:

• Support for Arbitrary-Length Nonces: Unlike traditional GCM, which supports only limited-length nonces, eGCM supports nonces of arbitrary length, providing greater flexibility in diverse application environments.
• Near-Perfect n-Bit Security: When the underlying block cipher is n-bit, eGCM provides nearly perfect n-bit security for a certain maximum input length, significantly improving upon the birthday bound (O(2^(n/2))) of traditional GCM.
• Similar Structure to GCM: eGCM maintains a structure similar to GCM, ensuring ease of implementation and compatibility. While the basic flow of encryption and authentication tag generation is similar to GCM, it internally uses eCTR and HteC to enhance security.
• Maintained Efficiency: Despite significant improvements in security, eGCM retains comparable efficiency in terms of rate and overall speed compared to GCM.

The operation of eGCM proceeds as follows:

• Nonce and additional authentication data (AAD) are processed through HteC to generate an initial state.
• This initial state is used to encrypt plaintext in eCTR mode.
• The ciphertext and AAD are processed through HteC to generate an authentication tag.

In this section, we provide formal definition of eGCM along with theoretical justifications for how it overcomes the limitations of GCM. Additionally, it includes a formal proof of eGCM's security.

eGCM-SIV Authenticated Encryption Scheme: Enhanced Security While Maintaining Resistance to Nonce Misuse

In this section, we propose eGCM-SIV, an enhanced variant of GCM-SIV. GCM-SIV is a variant of GCM that provides nonce misuse resistance, and eGCM-SIV maintains this feature while offering additional security enhancements.

The key features of eGCM-SIV are as follows:

• Nonce Misuse Resistance: Like GCM-SIV, eGCM-SIV provides nonce misuse resistance, ensuring confidentiality and authenticity of data even if a nonce is reused. This allows the scheme to maintain security even in cases where a nonce is accidentally reused.
• Support for Arbitrary-Length Nonces: Similar to eGCM, eGCM-SIV supports nonces of arbitrary length.
• Near-Perfect n-Bit Security: When the underlying block cipher is n-bit, eGCM-SIV provides nearly perfect n-bit security for a certain maximum input length.
• SIV(Synthetic Initialization Vector): Like GCM-SIV, eGCM-SIV employs the SIV method. In this approach, a synthetic initialization vector (SIV) is generated from the message-related data, and this SIV is used to encrypt a message.

The operation of eGCM-SIV proceeds as follows:

• Nonce, additional authentication data (AAD), and plaintext are processed through HteC to generate a synthetic initialization vector (SIV).
• This SIV is used to encrypt plaintext in eCTR mode.
• The SIV, along with the ciphertext, is output as the authentication tag.

In this section, we provide formal definition of eGCM-SIV along with theoretical justifications for how it overcomes the limitations of GCM-SIV. It also includes a formal proof of eGCM-SIV's security. Both eGCM and eGCM-SIV maintain the design philosophy of traditional GCM and GCM-SIV while significantly enhancing security and flexibility through new components such as eCTR and HteC. They are expected to play a crucial role in addressing the security requirements of modern cryptographic systems.

(Reference) Preliminary

Below is a separate compilation of knowledge to aid in understanding the document.

Basic Notation

In this section, we define mathematical notations and symbols used throughout the paper.

• Sets and Spaces: Notations for bit strings, blocks, key spaces, and other related entities.
• Function Notations: Methods of representing encryption functions, hash functions, pseudorandom functions, and similar constructs.
• Operators: Notations for operators such as XOR, concatenation, and bit shifts.
• Block Length: Notation for block length in an n-bit block cipher.

Security Notions

In this section, we discuss main cryptographic security concepts used in the paper.

• Pseudo-Random Function (PRF): A computable function that is indistinguishable from a randomly chosen function.
• Pseudo-Random Permutation (PRP): A computable permutation that is indistinguishable from a randomly chosen permutation.
• Tweakable Block Cipher (TBC): A block cipher with additional input (tweak).
• Authenticated Encryption with Associated Data (AEAD): An encryption scheme that simultaneously ensures confidentiality and authenticity of data.
• Birthday Bound: The threshold at which the probability of a collision becomes significantly high ($O(2^{n/2})$).

Coefficient-H Techniques

In this section, we discuss the Coefficient-H technique, a method used to prove the security of cryptographic primitives.

• Overview of the Technique: This method involves analyzing the distinguishability between the ideal world and the real world.
• Bad Transcripts and Good Transcripts: It categorizes scenarios where a distinguisher can differentiate between the ideal and real worlds, and cases where they cannot.
• Probability Analysis: The technique derives security bounds by calculating the probability of a bad transcript occurring.
• Applications: The Coefficient H-technique is applied to prove the security of eCTR and its derived modes.

Mirror Theory

In this section, we discuss mirror theory, a framework used to analyze the security of block cipher modes.

• Basic Concept of Mirror Theory: This theory focuses on analyzing the probability of internal state collisions occurring during encryption process.
• Collision Probability Analysis: It provides a method for calculating the probability of internal state collisions using mirror theory.
• Deriving Security Limits: The process involves deriving the security limits of an encryption mode through mirror theory.
• Application to eCTR: An explanation of how mirror theory is applied to analyze the security of eCTR.

Through this preliminary, we aim to provide background knowledge required to understand the design and security analysis of eCTR and its derived modes, the main contributions of the paper.