한 번만 써도 위험한 암호?
GCM의 한계를 극복하다

– 삼성SDS가 제안한 개선 기술

GCM인증 암호화 방식이란 무엇이며 삼성SDS의 접근방식은?

논문에서 주요하게 다루는 GCM 인증 암호화 방식은 세계에서 가장 널리 사용되는 AE(authenticated encryption) 방식 중 하나이지만, 논스 오용의 위험, 암호화당 짧은 메시지 길이, 그리고 불충분한 보안 수준과 같은 문제점을 가지고 있습니다. 본 논문의 목표는 GCM의 설계 원리를 바탕으로 표준 모델에서 더 강력한 증명 가능한 보안성을 달성하고 더 긴 논스(nonces)를 허용하는(또는 논스 오용에 대한 저항성을 제공하는) 새로운 AE 방식을 설계하는 것입니다.

그 결과, 논문에서는 GCM과 GCM-SIV의 두 가지 향상된 변형인 eGCM과 eGCM-SIV를 각각 제안하고 있습니다. eGCM과 eGCM-SIV는 eCTR이라 불리는 새로운 CENC 유형의 암호화 모드를 기반으로 구축되었습니다. 2n-비트 카운터를 사용하는 eCTR은 효율성의 상당한 손실 없이 생일 한계(Birthday Bound)를 초과하는 보안성을 제공합니다. eCTR은 거의 균일하고 거의 보편적인 해시 함수와 결합되어 HteC이라 불리는 가변 입력 길이 가변 출력 길이 의사 난수 함수를 생성합니다. GCM과 GCM-SIV는 eCTR과 HteC를 구성 요소로 사용하여 구축됩니다.

eGCM과 eGCM-SIV는 임의 길이의 논스를 허용하며, 기본 블록 암호가 의사 난수 순열(PRP) 이라는 가정 하에 일정한 최대 입력 길이에 대해 거의 완전한 보안성(즉, n-비트 블록 암호를 기반으로 할 때 n-비트 보안성)을 제공합니다. 또한 그 효율성은 속도와 전체 속도 측면에서 GCM과 비슷한 수준입니다.

* 생일 한계: 직관적으로 예상하는 것보다 훨씬 적은 수의 사람들에서 충돌이 발생한다는 의미로써, 암호학에서의 생일 한계는 n-비트 블록 암호나 해시 함수를 사용할 때 발생하는 보안 제한을 의미

삼성SDS의 핵심연구 키워드: eCTR, HteC, eGCM, eGCM-SIV

• eCTR(enhanced Counter Mode): 기존 CTR 모드의 생일 한계($O(2^{n/2})$)를 극복하고 거의 완전한 n-비트 보안($O(2^n)$)을 제공하는 향상된 카운터 모드를 제안
• HteC(Hash-then-eCTR): eCTR을 기반으로 하는 가변 입력 길이-가변 출력 길이(VIL-VOL) 의사 랜덤 함수(PRF)로, 거의 최적의 보안 수준을 제공
• eGCM(enhanced GCM): eCTR과 HteC를 기반으로 하는 GCM의 개선된 변형으로, 임의 길이 논스를 지원하고 향상된 보안 한계를 제공
• eGCM-SIV: 논스 오용에 강한 GCM-SIV의 개선된 변형으로, 논스 오용 저항성을 유지하면서 임의 길이 논스와 향상된 보안 한계를 제공

eCTR 기반 트윅가능 암호화 방식

본 논문에서는 eCTR을 기반으로 하는 트윅가능 암호화 방식(Tweakable Enciphering Schemes, TES)을 제안합니다.

• 트윅가능 암호화의 개념: 암호화 과정에 추가적인 매개변수(트윅)를 도입하여 유연성과 보안성을 향상시키는 방식
• 응용 분야: 제안된 트윅가능 암호화 방식은 디스크 암호화, 데이터베이스 암호화 등 다양한 분야에 적용 가능

eCTR: 완전한 보안성을 갖는 CTR 타입 연산 모드 [정리 1]

이 섹션에서는 기존 CTR 모드의 한계를 극복하는 새로운 암호화 모드인 eCTR(enhanced Counter Mode)을 소개합니다. 기존 CTR 모드는 생일 한계(O(2^(n/2)))에 의해 보안성이 제한되는 반면, eCTR은 거의 완전한 n-비트 보안(O(2^n))을 제공합니다.

eCTR의 주요 특징은 다음과 같습니다:

• 2n-비트 카운터를 사용하여 내부 상태 충돌 확률을 크게 감소시킴
• 블록 암호 호출 횟수를 최소화하여 효율성을 유지함
• 기존 CTR 모드와 유사한 구조를 유지하여 구현의 용이성을 보장함

eCTR의 작동 방식은 다음과 같습니다.

• 초기 카운터 값을 설정
• 각 블록 암호화마다 카운터 값을 증가
• 블록 암호를 사용하여 카운터 값을 암호화하고, 그 결과를 평문과 XOR하여 암호문을 생성

이 섹션에서는 eCTR의 형식적 정의와 함께, 그것이 어떻게 기존 CTR 모드의 생일 한계를 극복하는지에 대한 이론적 근거를 제시합니다. 또한 정리 1을 통해 eCTR의 보안성에 대한 형식적 주장을 제시합니다.

[정리 1]의 증명

이 섹션에서는 eCTR의 보안성에 관한 정리 1의 형식적 증명을 제공합니다. 증명은 다음과 같은 주요 단계로 구성됩니다.

• 계수-H 기법의 적용: 이상적 랜덤 함수와 eCTR 구현 간의 구별 가능성을 분석
• 나쁜 트랜스크립트 분석: 구별자가 이상적 세계와 실제 세계를 구별할 수 있는 경우를 식별
• 충돌 확률 계산: 2n-비트 카운터를 사용하여 내부상태 충돌 확률이 어떻게 감소하는지 계산
• 미러 이론 적용: 내부 상태의 충돌 확률을 분석하기 위해 미러 이론을 적용
• 최종 보안 한계 도출: 분석 결과를 종합하여 eCTR이 거의 n-비트 수준의 보안 제공을 증명

증명을 통해 eCTR이 기존 CTR 모드의 생일 한계를 극복하고 거의 완전한 n-비트 보안을 제공함을 수학적으로 보여줍니다.

HteC: 거의 최적으로 안전한 VIL-VOL PRF [정리 2]

이 섹션에서는 eCTR을 기반으로 하는 가변 입력 길이-가변 출력 길이(VIL-VOL) 의사 랜덤 함수인 HteC(Hash-then-eCTR)를 소개합니다. HteC는 다음과 같은 두 가지 주요 구성 요소로 이루어집니다

• 거의 균일하고 거의 보편적인 해시 함수(AXU 해시): 임의 길이의 입력을 고정 길이의 해시 값으로 변환
• eCTR: 해시 값을 사용하여 원하는 길이의 출력을 생성

HteC의 작동 방식은 다음과 같습니다.

• 입력 메시지를 AXU 해시 함수를 사용하여 해시
• 해시 값을 eCTR의 초기 카운터 값으로 사용
• eCTR을 사용하여 원하는 길이의 출력을 생성

이 섹션에서는 HteC의 형식적 정의와 함께, 그것이 어떻게 거의 최적의 보안 수준을 달성 하는지에 대한 이론적 근거를 제시합니다. 또한 정리 2를 통해 HteC의 보안성에 대한 형식적 주장을 제시합니다.

[정리 2]의 증명

이 섹션에서는 HteC의 보안성에 관한 정리 2의 형식적 증명을 제공합니다. 증명은 다음과 같은 주요 단계로 구성됩니다:

• HteC의 구조 분석: HteC가 어떻게 AXU 해시 함수와 eCTR을 결합하는지 분석
• AXU 해시 함수의 특성 활용: 거의 균일하고 거의 보편적인 해시 함수의 특성이 어떻게 보안성에 기여하는지 분석
• eCTR의 보안성 활용: [정리 1]에서 증명된 eCTR의 보안성이 어떻게 HteC의 보안성에 기여하는지 분석
• 하이브리드 인수 적용: 이상적 해시 함수와 실제 해시 함수 간의 차이를 분석하기 위해 하이브리드 인수를 적용
• 최종 보안 한계 도출: 분석 결과를 종합하여 HteC가 최적의 보안 수준을 제공함을 증명

증명을 통해 HteC가 가변 입력 길이-가변 출력 길이 의사 랜덤 함수로서 거의 최적의 보안 수준을 달성함을 수학적으로 보여줍니다. 이는 eGCM과 eGCM-SIV의 보안성을 위한 중요한 기반이 됩니다.
이 섹션에서 제시된 eCTR과 HteC는 논문의 주요 기여인 eGCM과 eGCM-SIV의 핵심 구성 요소로, 이후 섹션에서 이 두 구성 요소를 기반으로 eGCM과 eGCM-SIV가 어떻게 구축되는지 설명합니다

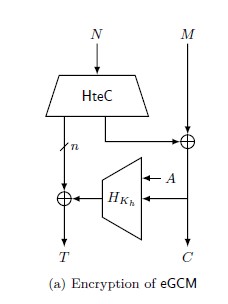
eGCM 인증 암호화 방식: GCM의 한계를 극복하면서도 효율적인 암호

이 섹션에서는 기존 GCM(Galois/Counter Mode)의 향상된 변형인 eGCM(enhanced GCM)을 소개합니다. eGCM은 앞서 설명한 eCTR과 HteC를 기반으로 구축되어, GCM의 여러 한계점을 극복하면서도 그 설계 철학과 효율성을 유지합니다.

eGCM의 주요 특징은 다음과 같습니다.

• 임의 길이의 논스 지원: 기존 GCM이 제한된 길이의 논스만을 지원하는 것과 달리, eGCM은 임의 길이의 논스를 지원합니다. 이는 다양한 응용 환경에서 더 큰 유연성을 제공
• 거의 완전한 n-비트 보안: eGCM은 기저 블록 암호가 n-비트일 때, 일정한 최대 입력 길이에 대해 거의 n-비트에 가까운 완전한 보안을 제공합니다. 이는 기존 GCM의 생일 한계(O(2^(n/2)))를 크게 개선한 것
• GCM과 유사한 구조: eGCM은 GCM과 유사한 구조를 유지하여 구현의 용이성과 호환성을 보장합니다. 암호화와 인증 태그 생성의 기본 흐름은 GCM과 유사하지만, 내부적으로 eCTR과 HteC를 사용하여 보안성을 향상
• 효율성 유지: eGCM은 보안성이 크게 향상되었음에도 불구하고, 처리율과 전체 속도 측면에서 GCM과 비교 가능한 효율성을 유지

eGCM의 작동 방식은 다음과 같습니다.

• 논스와 추가 인증 데이터(AAD)를 HteC를 통해 처리하여 초기 상태를 생성
• 이 초기 상태를 사용하여 eCTR 모드로 평문을 암호화
• 암호문과 AAD를 HteC를 통해 처리하여 인증 태그를 생성

이 섹션에서는 eGCM의 형식적 정의와 함께, 그것이 어떻게 GCM의 한계를 극복하는지에 대한 이론적 근거를 제시합니다. 또한 eGCM의 보안성에 대한 형식적 증명도 제공합니다.

eGCM-SIV 인증 암호화 방식: 논스 오용의 저항성을 유지하면서도 보안은 향상

이 섹션에서는 GCM-SIV의 향상된 변형인 eGCM-SIV를 소개합니다. GCM-SIV는 논스 오용 저항성(nonce misuse resistance)을 제공하는 GCM의 변형으로, eGCM-SIV는 이러한 논스 오용 저항성을 유지하면서도 추가적인 보안 향상을 제공합니다.

eGCM-SIV의 주요 특징은 다음과 같습니다.

• 논스 오용 저항성: eGCM-SIV는 GCM-SIV와 마찬가지로 논스가 재사용되더라도 기밀성과 무결성을 유지하는 논스 오용 저항성을 제공합니다. 이는 실수로 논스가 재사용되는 상황에서도 보안성을 유지할 수 있도록 지원
• 임의 길이의 논스 지원: eGCM-SIV도 eGCM과 마찬가지로 임의 길이의 논스를 지원
• 거의 완전한 n-비트 보안: eGCM-SIV는 기저 블록 암호가 n-비트일 때, 일정한 최대 입력 길이에 대해 거의 n-비트에 가까운 완전한 보안을 제공
• SIV(Synthetic Initialization Vector) 방식: eGCM-SIV는 GCM-SIV와 마찬가지로 SIV 방식을 사용합니다. 이 방식에서는 메시지 관련 데이터로부터 합성 초기화 벡터(SIV)를 생성하고,이 SIV를 사용하여 메시지를 암호화

eGCM-SIV의 작동 방식은 다음과 같습니다.

• 논스, 추가 인증 데이터(AAD), 그리고 평문을 HteC를 통해 처리하여 합성 초기화 벡터(SIV)를 생성
• 이 SIV를 사용하여 eCTR 모드로 평문을 암호화
• 암호문과 함께 SIV를 인증 태그로 출력

이 섹션에서는 eGCM-SIV의 형식적 정의와 함께, 그것이 어떻게 GCM-SIV의 한계를 극복하는지에 대한 이론적 근거를 제시합니다. 또한 eGCM-SIV의 보안성에 대한 형식적 증명도 제공합니다. eGCM과 eGCM-SIV는 모두 기존 GCM과 GCM-SIV의 설계 철학을 유지하면서도, eCTR과 HteC라는 새로운 구성 요소를 통해 보안성과 유연성을 크게 향상시킵니다. 이들은 현대 암호화 시스템의 보안 요구사항을 충족시키는 데 중요한 기여를 할 것으로 기대됩니다.

(참고) 예비 지식

문서 이해를 돕기위한 지식을 별도로 정리해 보았습니다.

본 표기법 (Basic Notation)

이 섹션에서는 논문 전체에서 사용되는 수학적 표기법과 기호들을 정의합니다

• 집합과 공간: 비트열, 블록, 키 공간 등에 대한 표기법
• 함수 표기법: 암호화 함수, 해시 함수, 의사 랜덤 함수 등의 표기 방법
• 연산자: XOR, 연결, 비트 시프트 등의 연산자 표기
• 블록 길이: n-비트 블록 암호에서의 블록 길이 표기

보안 개념 (Security Notions)

이 섹션에서는 논문에서 사용되는 주요 암호학적 보안 개념을 설명합니다

• 의사 랜덤 함수(PRF): 랜덤하게 선택된 함수와 구별할 수 없는 효율적으로 계산 가능한 함수
• 의사 랜덤 치환(PRP): 랜덤하게 선택된 치환과 구별할 수 없는 효율적으로 계산 가능한 치환
• 트윅가능 블록 암호(TBC): 추가적인 입력(트윅)을 받는 블록 암호
• 인증 암호화(AEAD): 기밀성과 무결성을 동시에 제공하는 암호화 방식
• 생일 한계(Birthday Bound): 충돌 확률이 상당히 높아지는 지점($O(2^{n/2})$)

계수-H 기법 (Coefficient-H Technique)

이 섹션에서는 암호 프리미티브의 보안성을 증명하는 데 사용되는 계수-H 기법을 설명합니다.

• 기법의 개요: 이상적 세계와 실제 세계 간의 구별 가능성을 분석하는 방법
• 나쁜 트랜스크립트와 좋은 트랜스크립트: 구별자가 이상적 세계와 실제 세계를 구별할 수 있는 경우와 그렇지 않은 경우
• 확률 분석: 나쁜 트랜스크립트가 발생할 확률을 계산하여 보안 한계를 도출하는 방법
• 응용: 이 기법이 eCTR과 그 파생 모드의 보안성 증명에 어떻게 적용되는지 설명

미러 이론 (Mirror Theory)

이 섹션에서는 블록 암호 모드의 보안성 분석에 사용되는 미러 이론을 설명합니다.

• 미러 이론의 기본 개념: 암호화 과정에서 발생하는 내부 상태의 충돌 확률을 분석하는 이론
• 충돌 확률 분석: 미러 이론을 사용하여 내부 상태 충돌 확률을 계산하는 방법
• 보안 한계 도출: 미러 이론을 통해 암호화 모드의 보안 한계를 도출하는 과정
• eCTR에의 적용: 미러 이론이 eCTR의 보안성 분석에 어떻게 적용되는지 설명

Preliminary을 통해 논문의 주요 기여인 eCTR과 그 파생 모드들의 설계와 보안성 분석을 이해하기 위한 필수적인 배경 지식을 제공하고자 하였습니다.