인공지능을 사용한 순차 데이터 분석
순차 데이터
순차 데이터란 ‘데이터 집합 내의 객체들이 어떤 순서를 가진 데이터’로, 그 순서가 변경될 경우 고유의 특성을 잃어버리는 특징이 있습니다. 쉬운 예로, ‘도’와 ‘시’라는 글자 객체들로 ‘도시’와 ‘시도’라는 단어들의 조합이 가능하지만 이들은 서로 다른 의미를 갖는 것과 같습니다. 이처럼 우리가 사용하는 언어는 물론, IoT 기기에서 생성되는 센서 데이터, 주가 변동, 지진파, 그리고 DNA 염기서열 등 수없이 많은 종류의 시계열 데이터(time-series data)는 모두 순차 데이터에 포함됩니다. 실제 산업 현장에는 매우 다양한 형태의 순차 데이터들이 엄청난 규모로 발생하고 있으며, 최근 회자되는 4차 산업혁명의 핵심은 이러한 데이터에서 인사이트를 도출하는 것입니다. 이번 리포트에서는 순차 데이터를 분석하는 기본 방법과 최근 인공지능을 활용한 분석 사례를 설명하겠습니다.
고전적인 순차 데이터 분석 – 은닉 마코프 모델(Hidden Markov Model)
[아래 설명은 전북대학교 전자정보공학부 컴퓨터공학 교수 오일석의 ≪패턴인식(교보문고, 2008) ≫을 참고했습니다. 보다 상세한 내용은 해당 도서를 포함한 관련 교재를 참조하시기 바랍니다.]
순차 데이터를 분석하기 위해서는 먼저, 데이터의 시간적인 특성(temporal property 또는 전후 관계)을 나타낼 수 있는 표현 방법이 필요하고, 다음으로 그 데이터에서 정보를 추론(예측)할 수 있는 방법이 필요합니다. 그럼, 먼저 길이가 T 인 가변 길이(variable length) 순차 데이터의 표현 방법을 설명하겠습니다.
(식1)에서 O 는 전체 순차 데이터를 나타내고(observations), O 의 각 원소 oi는 i 시점의 관측(observation)을 의미합니다. 이때, 각 관측 oi는 집합 V={v₁,v₁,⋯,vm}의 한 원소를 상태(state) 값으로 갖게 됩니다. 예를 들어, 날씨의 상태를 나타내는 집합 V = {비, 구름, 해}가 있을 때, 해가 뜬 오늘 (t)의 날씨(ot)는 ‘ot=해’로 표현됩니다.
다음으로, 순차 데이터에서 정보를 추론하는 방법을 설명해 보겠습니다. 러시아의 수학자 Andrey Andreyevich Markov(1856~1922)는‘시간 t 에서의 관측은 가장 최근의 관측 r 개에만 의존한다’는 가정에 기반을 둔 확률 추론 모델인 마코프 연쇄(Markov chain)를 제안했습니다. 이를 식으로 표현하면 (식2)와 같습니다.
r=1: P(0t│0t-1 0t-2⋯01)=P(0t |0t-1) (식2)
r=2: P(0t│0t-10t-2⋯01)=P(0t |0t-1 0t-2)
(식2)를 바탕으로 ‘r=1’인 마코프 연쇄(1차 마코프 연쇄)로 위의 날씨 상태 예제를 모델링하고, 간단한 예측을 해보겠습니다. 기후 관측에 의해 얻은 날씨 변화의 확률이 [표1]과 같다고 할 때, 위 예제는 [그림1]와 같은 (a)상태 전이 확률 행렬과 (b)상태 전이도로 모델링 할 수 있습니다.
 |
비 | 구름 | 해 |
|---|---|---|---|
| 비 | 0.4 | 0.3 | 0.3 |
| 구름 | 0.2 | 0.6 | 0.2 |
| 해 | 0.1 | 0.1 | 0.8 |
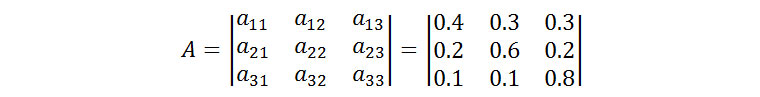 (a) 상태 전이 확률 행렬
(a) 상태 전이 확률 행렬
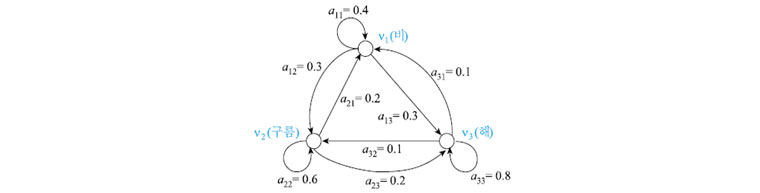 (b) 상태 전이도
(b) 상태 전이도[그림1] 1차 마코프 모델을 위한 상태 전이 확률과 상태 전이도
이 모델을 기반으로‘오늘은 해가 떴지만 내일부터 7일간의 날씨가 해-해-비-비-해-구름-해’인 경우를 예측해(즉, 확률을 구해) 보겠습니다. 오늘 해가 뜬 확률을 ‘P(해)=1.0’로 하면, 주어진 날씨 순서대로 이후 7일 동안의 날씨가 나타날 확률 P(해해해비비해구름해)는 아래와 같습니다.
=1*a₃₃*a₃₃*a₃₁*a₁₁*a₁₃*a₃₂*a₂₃
=1*0.8*0.8*0.1*0.4*0.3*0.1*0.2
=1.536*10-⁴
지금까지 설명한 1차 마코프 연쇄는 직관적이어서 이해하기는 쉽지만, 더 많은 이전 관측을 필요로 하는 현실에서의 응용에는 한계가 있습니다. 즉, 2차 이상의 마코프 연쇄에서는 상태의 수가 급증하므로(날씨 예의 경우, 1차 마코프 연쇄 3²→ 2차 마코프 연쇄 3³→ 3차 마코프 연쇄 3⁴) 복잡한 현상에 대한 모델링이 매우 어렵습니다. 때문에, 음성인식과 같은 실제 문제에서는 이러한 제약을 완화하는 은닉 마코프 모델(Hidden Markov Model)이 널리 사용됩니다. 은닉 마코프 모델은 마코프 모델을 근간으로 하고 있으며, 차수를 미리 고정하지 않고 확률 프로세스에 따라 적응적으로 모델이 결정되기 때문에, 먼 과거의 관측이 현재의 상태에 영향을 미치도록 모델링 할 수 있습니다.
은닉 마코프 모델은 내용이 꽤 방대하므로 본 포스트에서는 상세한 설명을 생략하겠습니다. 관심 있는 분들은 위의 참고문헌을 참조하시기 바랍니다.

인공지능을 사용한 순차 데이터 분석
음성인식(speech to text) 기술은 [그림2]와 같이 시계열 데이터인 음성(speech)의 패턴을 분석하여, 음성에서 텍스트를 예측하는 기술입니다. 그동안 음성인식 분야에서는 시간적 특성을 가진 음성을 대상으로, 앞서 설명한 은닉 마코프 모델을 적용하여 텍스트를 유추하려 노력해왔습니다. 예를 들어, “여”라는 음성 뒤에 “우”라는 음성이 나타날 확률이 “큐”라는 음성이 나올 확률보다 더 크다는 관찰 결과를 이용하는 것이죠.
 [그림2] “여우” 음성의 웨이브 형태
[그림2] “여우” 음성의 웨이브 형태(출처: “인공지능 기반의 음성인식 기술개발동향과 도입방안 및 전략 세미나,” 서강대 김지환 교수, Mar. 2017)
하지만, 1950년대부터 개발된 음성인식 기술은 2000년대 초까지도 연속된 몇 개의 단어를 인식하는 수준에서 벗어나지 못했습니다. 긴 문장을 모델링 하기에는 은닉 마코프 모델이 너무 복잡하고, 모델링에 사용되는 학습 데이터의 양도 적어서 인식 성능이 지나치게 화자(speaker)에 종속적이었기 때문입니다.
그러다 최근(2010년대 후반) 화자에 관계없이 높은 인식 성능을 바탕으로 [그림3]의 인공지능 스피커와 같은 불특정 다수를 위한 서비스가 가능해졌는데, 이는 딥러닝의 활용 덕분입니다.
 [그림3] 다양한 인공지능 스피커들
[그림3] 다양한 인공지능 스피커들
RNN (Recurrent Neural Network), LSTM (Long Short-Term Memory), GRU (Gated Recurrent Unit) 등의 딥러닝 알고리즘들은 인공신경망이 순차 데이터의 순서를 유지하면서도([그림4]) 매우 많은 분량의 학습 데이터를 학습할 수 있도록 고안되어, 앞서 말씀 드린 은닉 마코프 모델의 문제점들을 해결했습니다. 또한, CPU, GPU, 메모리 등의 연산 능력과 분산 컴퓨팅 기술의 비약적인 발전으로 복잡한 확률 계산과 빅데이터 처리가 가능해지면서 실생활에서 활용 가능한 다양한 순차 데이터 처리가 가능해 졌습니다(예: 음성인식, 자연어처리, 기계번역, 의료신호 분석, 판매량 예측 등).
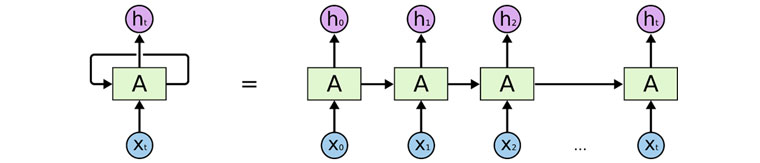 [그림4] RNN 구조
[그림4] RNN 구조(출처: https://colah.github.io/posts/2015-08-Understanding-LSTMs/)
빅데이터와 사물인터넷, 그리고 딥러닝 기술의 발전으로 이전에는 불가능했던 다양한 종류의 순차 데이터 분석이 가능해졌습니다. 앞서 말했지만 이를 통해 인사이트를 도출하여 비즈니스에 적용하는 것이 바로 4차 산업혁명의 핵심입니다.
▶ 해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에 저작권이 있습니다.
▶ 해당 콘텐츠는 사전 동의없이 2차 가공 및 영리적인 이용을 금하고 있습니다.

삼성SDS AI선행연구Lab
KAIST에서 데이터베이스와 데이터마이닝을 전공하여 박사학위를 취득했습니다. 이후 BI플랫폼 개발과 다양한 데이터 분석을 진행했으며, 현재는 연구소 AI선행연구Lab에서 자연어이해와 이미지인식을 기반으로 하는 엔터프라이즈 AI, 데이터 분석 기술을 연구, 개발하고 있습니다.