실생활에서 AI를 많이들 사용하고 계신가요? 이제는 ChatGPT 혹은 Gemini 등 다양한 LLM(Large Language Model) 기반의 챗봇과 자연스러운 대화를 통해 회사 업무든 개인적인 일이든 도움을 받는 것이 더 이상 신기한 일은 아닙니다. 하지만, 2023년 1월에 ChatGPT를 처음 접했을 때 놀랐던 기억이 아직도 생생합니다. 당시 새로운 AI가 공개됐다는 소식에 별 기대 없이 테스트를 해보는데, 처음엔 ‘사전에 정해진 몇몇 단어에 대해 정해진 답변을 하는 정도겠지’라는 생각을 했습니다. (예를 들면 사용자의 질문에 "비", "날씨", "온도/기온", "춥다/덥다", "우산" 등의 단어가 포함되어 있으면 날씨 정보를 제공하는 식) 그러나, 별 기대 없이 던진 질문에 예상외의 답변을 하는 것을 보고 "이게 뭐지?" 하는 신기함을 넘어 전율을 느꼈던 기억이 납니다.
언어(단어)를 숫자로 표현하기
사실 LLM 기반의 AI가 만들어낸 결과물의 파장은 어마어마하지만, 이것을 가능케 한 연구 개발의 역사는 생각보다 오래된 것은 아닙니다. 관련된 중요한 결과물들은 대부분 10년 정도밖에 되지 않았으니까요. 그러니, 조금만 더 일찍 관심을 가졌다면 우리도 뭔가를 만들어낼 수 있었을까요? :-) 그렇다면 우리가 연구자라고 가정하고 그들의 발자국을 따라가 보도록 하겠습니다.
일단 컴퓨터상에서 언어를 표현하려면 어찌 됐든 숫자로 변환/표현이 되어야 합니다. 이것에 대해서는 부가 설명은 필요 없을 겁니다. 그럼, 이제 언어 그 중에서도 가장 기본이 되는 요소인 개별 단어를 숫자로 표현하는 방법에 대해 생각해 보겠습니다.
일단 단어를 숫자로 표현하는 방법 중 가장 쉬운 방법은, 단어에 일련번호를 붙이는 것이 될 겁니다. 이때 전체 단어 목록의 확보 및 각 단어에 번호를 붙이는 순서를 정하려면 뭔가 기준이 필요하니, 세계적으로 권위 있는 옥스퍼드 사전에 등록된 단어를 기준으로 알파벳 순서에 따라 번호를 매겨 봅니다. 참고로 옥스퍼드 사전엔 현재 10만 개가 넘는 단어가 등록되어 있다고 합니다. 그렇게 되면 1번부터 시작해 10만 번째 번호가 붙은 단어 목록이 생길 것입니다. 이제 이 목록을 기준으로 입력된 문장의 단어를 숫자로 치환하고 신경망(LLM, 언어모델)에 입력하면 어떻게 될까요? 우리가 원하는 답을 얻을 수 있을까요?
불행히도 그렇게 되진 않습니다. 그 이유는…. 사실 우리가 단어에 일련번호를 붙일 때의 의도는 '숫자의 모습'을 갖고 있었지만, 암묵적으로 숫자의 크고 작음은 아무 의미가 없고 단지 '구분자(Unique Identifier)'라는 의미로 사용됐습니다. 하지만, 이 숫자 데이터는 언어모델에 입력되면 일반 숫자와 똑같이 '구분자'가 아니라 '크기'의 의미를 갖는 숫자로 취급되며, 그 크기에 따라 어떤 "강도(Intensity)" 혹은 "경향(Inclination)"의 성질이 나타나게 됩니다. 즉 우리는 의도하지 않았지만, 1번 단어 대비 10만 번째 단어에는 어떤 강도나 경향이 10만 배 더 부여되어 엉뚱한 결과를 만들게 됩니다. 게다가 거기에 수십, 수만 번의 곱하기와 더하기 등을 거치면 그 강도와 경향은 더 증폭될 겁니다.
그렇다면 각 단어를 대표하는 임의의 숫자가 강도/경향을 나타내지 않으면서 어떻게 해야 구분자로서의 의미만을 표현할 수 있을까요? 아이디어가 떠오르시나요? 바로 벡터를 사용하는 것입니다. 방법은 이렇습니다. 예를 들어 우리의 AI가 단지 딱 3개 단어만 이해/구사하는 것으로 가정하고 ‘Apple, Grape, Car’라는 단어를 대상으로 한다면, 전체 단어가 3개이니 각 단어는 3차원의 벡터로 표현하여 Apple은 [1, 0, 0], Grape는 [0, 1, 0], 그리고 Car는 [0, 0, 1]로 표현하는 겁니다. 이 경우, 각 단어를 표현하는 벡터에서 가장 큰 값은 "1"로 3개 단어 모두가 같지만, 각 단어를 Unique하게 표현할 수 있습니다. 참고로 이런 방식을 One-Hot Encoding이라고 합니다.
그럼, 조금 전 옥스퍼드 사전으로 돌아가서, 각 단어를 One-Hot Encoding을 하게 되면 어떻게 될까요? 각각의 모든 단어는 10만 차원의 벡터로 표현이 됩니다. 그래서 첫 번째 단어를 벡터로 표현하면, [1, 0, 0, 0…. 0] 이렇게 됩니다. 첫 번째 숫자만 1이고 나머지 99,999개는 모두 0인 벡터. 그리고 마지막 단어는 [0, 0, 0…. 1]이 됩니다.
흠…. 뭔가 이상하다는 생각이 드시나요? 물론, 어차피 컴퓨터가 계산하는 일인데 이 정도는 할 수 있지 않을까 하시겠지만, 여기에 한국어도 포함되고, 프랑스어도 포함되고, 독일어도 포함되고…. 자연어 처리(NLP, Natural Language Processing)가 목표로 했던 주요 Application 중 하나가 언어 번역인 것을 생각하면, 단어 하나를 표현하는 데 수십만 차원의 벡터가 필요해지는 겁니다. 그것도 단 한 개의 숫자만 1이고 나머진 모두 0인 벡터로요. 당연히 메모리상으로 비효율적이고, 0은 수백만 번의 곱셈 연산을 해도 0이 되는 의미 없는 연산을 해야 하는 등의 문제점을 갖고 있었습니다.
참고) One-Hot-Encoding처럼 벡터가 대부분 0으로 채워진 것을 희소 벡터(Sparse Vector)라고 합니다.
게다가, 이 방법은 Computing 측면에서 비효율이라는 문제뿐만 아니라 또 다른 더 큰 근본적인 문제점을 가지고 있는데, 그것은 각 벡터에 해당 단어가 갖고 있는 언어적 "의미(Meaning)" 정보를 담고 있지 않다는 것입니다. 즉 단어를 숫자로 표현했을 뿐 그 단어 고유의 의미 정보를 담고 있지 않습니다. 이로 인해 이 방법을 사용한 언어모델들의 성능이 좋지 않았습니다.
참고) 이 당시에는 오늘날 LLM들이 사용하는 Transformer 아키텍처 기반이 아닌 RNN(혹은 RNN의 변형)을 기반으로 한 언어모델로 그 자체로도 성능이 낮았음.
그럼, 이를 해결하는 방법은 뭐가 있을까요? 각 단어 고유의 의미를 숫자로 담으면서 동시에 수십만 차원의 벡터가 필요하지 않는 .... 이와 관련해서 RGB 색상 체계를 생각해 봅니다. RGB 색상 체계는 이름이 의미하듯 Red, Green, Blue 3원색을 기본색으로 하여 이들 간의 조합으로 어떤 색을 만드는 혹은 정의하는 방법입니다. 이 RGB 체계는 컴퓨터에서 많이 사용되고 있는데요. 이 3원색은 각각 0부터 255 사이의 정수값으로 표현되는 강도(Intensity)를 가지며, 숫자가 커질수록 해당 색깔 성분의 강도가 커집니다. 이를 통해 어떠한 색이든 3차원 벡터로 표현될 수 있어, 예를 들면 빨간색은 (255, 0, 0), 파란색은 (0, 255, 0)이 되며, 초록색은 (0, 0, 255)으로 표현됩니다. 그래서 표현할 수 있는 전체 색깔은 이론적으론 256 x 256 x 256 = 16,777,216개가 됩니다. 즉 3차원 벡터 한 개로 천만 개가 넘는 색(흔히 True Color라고 함, 8비트)을 명확하게 지정, 표현할 수 있게 되는 것입니다. 이 방법은 각 벡터 내 원소/성분이 0부터 255까지 숫자를 가질 수 있지만, 처음에 예시한 아무 의미 없는 일련번호 1~10만 번과는 달리 각 숫자의 크기가 의미를 담고 있어 곱하기, 더하기 연산을 통해서 나오는 값은 실제 그 경향의 크기를 반영하기 때문에 문제가 없습니다.
한편, 이렇게 색깔을 정의하게 되면, 또 다른 장점이 생기는데 바로 색깔 간 '계산'을 할 수 있게 된다는 점입니다. 예를 들면 색깔 간 '더하기(혼합)'를 할 수 있어서, 빨강과 초록을 섞는다고 하면 이는 벡터 연산 방식에 따라서 노란색을 '계산'해 낼 수 있습니다. 이를 더 발전시키면 3D 그래픽스 혹은 게임 등에서 빛에 반사되는 물체들의 색깔들을 자연스럽게 그리고 실제 현실 세계와 비슷한 모습을 만들어낼 수 있게 됩니다.
 [그림 1] ‘노란색’ 벡터 계산식
[그림 1] ‘노란색’ 벡터 계산식
그럼 이 아이디어를 우리의 언어에도 응용할 수 있을까요? 구체적으로 …. (사과, 배, 오렌지, 블루베리, 딸기, 포도, 수박) 이렇게 7개의 과일 단어에 대해 생각해 보겠습니다. 이제 위의 일련번호를 붙이기나 One-Hot-Encoding의 경우처럼 아무 의미 없는 숫자의 배정이 아닌, RGB처럼 색을 정의하는 3가지의 원소 혹은 기준을 사용했듯이, 과일의 외형을 구분하는 기준을 떠올려 봅니다. 일단 '크기', '색깔', '무게' 정도가 있을 거 같습니다. 그럼, 그 관점별로 7개 과일을 평가해 보겠습니다.
<표 1> 과일별 벡터 표현
| 구분 | 사과 | 배 | 오렌지 | 블루베리 | 딸기 | 포도(알) | 수박 |
|---|---|---|---|---|---|---|---|
| 크기(지름, cm) | 10 | 13 | 8 | 1 | 3 | 2 | 30 |
| 색깔(빨강 1, 파랑 2, 노랑 3) | 1 | 3 | 3 | 2 | 1 | 2 | 1 |
| 무게(kg) | 0.2 | 0.5 | 0.2 | 0.002 | 0.03 | 0.01 | 3 |
| 벡터 표현 | (10, 1, 02) | (13, 3, 0.5) | (8, 3, 0.2) | (1, 2, 0.002) | (3, 1, 0.03) | (2, 2, 0.01) | (30, 1, 3) |
이렇게 해보니 3차원 벡터로 7개 과일을 Unique하게 표현할 수 있게 되었습니다. 실은, 이 방법을 통해서 다른 수많은 과일도 3차원 벡터로 얼마든지 표현할 수 있을 거 같습니다. (혹은 목적에 따라 맛, 당도 등의 추가적인 차원 또는 기준을 추가해도 될 듯 합니다.) 즉, One-Hot Encoding보다 Computing 관점에서 훨씬 효율적이고, 동시에 각 차원의 숫자가 그 과일의 특성을 담고 있어서, 언어모델에 사용 시 더 좋은 결과를 만들어낼 수 있게 될 것입니다. 참고로, 이와 같이 단어를 벡터로 표현하는 것(A vector representation of a word)을 통칭하여 임베딩(Embedding)이라고 합니다.
두 벡터 간 유사도 계산
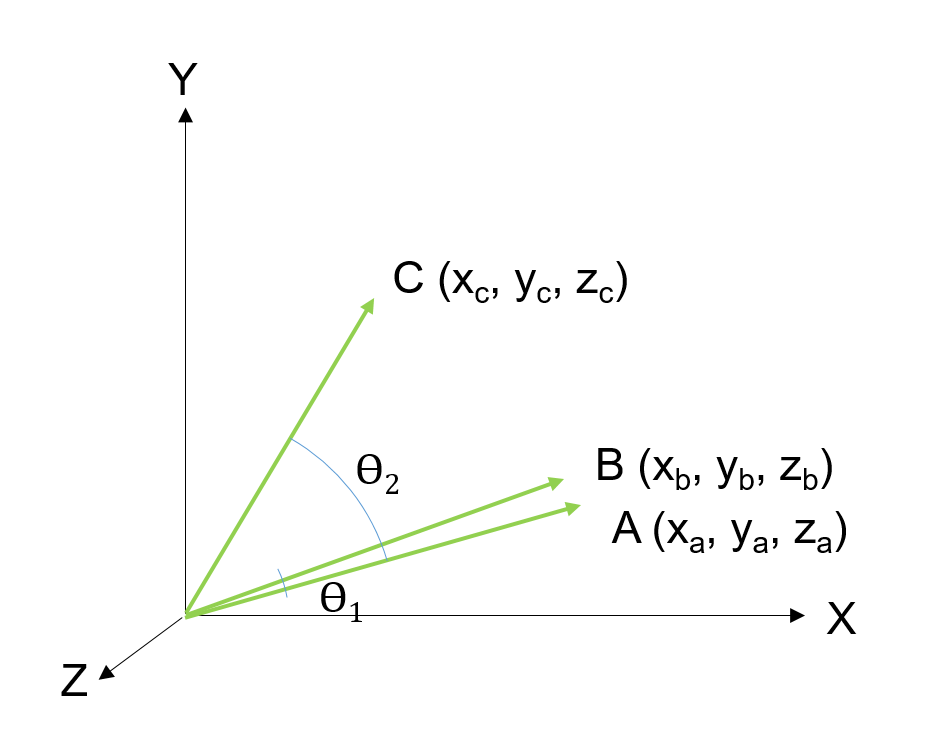 [그림 2] 벡터 간 유사도 그래프
[그림 2] 벡터 간 유사도 그래프
벡터 A, B, C 중에서 벡터 A와 비슷한 것은 벡터 B입니다. 이를 판정하는 대표적인 방법은 아래의 두 가지 방법이 있습니다.
(1) 거리 측정(Euclidean Distance)
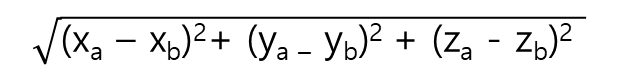 [그림 3] 벡터 간 거리 측정 공식
[그림 3] 벡터 간 거리 측정 공식
(2) 각도 측정(Cosine Similarity)
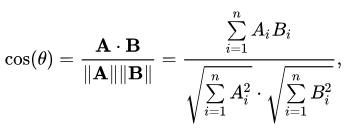 [그림 4] 벡터 간 각도 측정 공식
[그림 4] 벡터 간 각도 측정 공식
위와 같은 방식으로 과일 단어들이 임베딩되고 나면 각 단어가 숫자로 정의되었다는 것 이외에 재미있는 응용처가 생깁니다. 바로 비슷하게 생긴 과일(이름) 찾기입니다. 여기서 강조하는 점은 같은 이름의 과일 검색이 아닌 '외형이 비슷한' 과일입니다. 우리가 일상적으로 접하는 동일어 검색 즉 주어진 이름과 같은 이름의 과일 이름 검색은 구현하기 쉽습니다. 주어진 단어에 대해 위의 7개 과일 이름을 하나씩 비교해서 일치하는지 판단하면 되니까요. 우리가 현재 사용하는 네이버, 구글 검색도 다 동일어 검색입니다. 검색하고자 하는 단어와 동일한 단어가 포함된 웹페이지를 찾아줍니다.
하지만, 비슷하게 생긴 과일 검색은 완전히 다른 이야기입니다. 여기서 말하는 비슷한 외형의 과일 검색이라는 것은 7개의 과일 중에서 예를 들면 포도(알)과 가장 비슷하게 생긴 과일, 즉 블루베리를 찾아내는 것을 말합니다. 그런데 실제로도 위의 표를 자세히 보시면 포도(알)의 벡터값과 가장 유사한 벡터를 갖는 것은 블루베리라는 것을 알 수 있습니다. 물론 이것은 과일의 외형을 기준으로 임베딩을 만들었기 때문입니다.
그렇다면, 두 벡터가 비슷하다는 것(그 두 벡터로 지칭되는 단어의 의미가 비슷하다는 것)을 어떻게 판별을 할 수 있을까요? 두 벡터가 얼마나 비슷한가를 나타낼 때 사용하는 것을 유사도(Similarity)라고 하는데, 흔히 두 벡터의 유사도는 두 벡터의 끝점 간 거리를 계산하거나 혹은 원점을 기준으로 두 벡터 간 각도를 계산하는 방법 등이 사용됩니다. (거리가 짧거나 각도가 작으면 서로 유사한 위치에 있는 벡터입니다.) 특히 이 중에서 두 벡터 간 각도를 계산하는 방법이 언어 관련 시스템에서 많이 사용되는데 이때 사용되는 방법이 코사인 유사도(Cosine Similarity)입니다. 이를 활용해 벡터 간 유사도를 계산하면 가장 유사한 단어가 무엇인지를 "계산"으로 알아낼 수 있습니다.
자, 그럼 이제 우리가 찾던 답을 찾은 건가요? 가능성이 보이긴 하나 불행히도 예시처럼 아주 작은 범주의 단어가 아닌 우리가 사용하는 모든 개별 단어를 이런 식으로 일일이 정의하는 것이 현실적으로 불가능합니다. '자동차', '사람', '영국', '암석', '바이러스', '고래', '아름답다', '춥다', '어렵다' 같이 어려운 단어가 아닌 우리 일상에서 사용하는 평범한 단어 9개를 구분 또는 정의할 수 있는 적절한 기준과 관점을 만들기는 상당히 어렵습니다. 심지어 그 기준/관점을 300개 정도로 늘린다고 해도요. 물론 그 기준/관점은 상호 간 겹치는 부분이 있어서는 안 되고 그 기준에 맞게 제대로 분류하는 것도 쉽지 않을 겁니다. 그리고 이걸 관련된 모든 사람이 동의해야 하는 것도 있고요. 그래서 사실 기준/관점이라고 표현했지만 결국은 분류체계를 만드는 겁니다. 그리고 단어에 대한 분류체계지만, 실상은 이 세상 삼라만상 "모든 것"에 대한 통합된 만능 분류체계를 만들어야 하는 것이기 때문에 거의 불가능에 가깝습니다. 하지만, 여기서 우리는 단어를 숫자로 표현하는 데 있어 하나의 실마리를 찾은 거 같습니다. 바로.... "단어의 특징을 숫자로 담고 있는 저차원(低次元, Low Dimension)의 밀집(Dense) 벡터"입니다.
Word2Vec
단어를 숫자로 표현하고자 할 때 필요한 조건에 대해서 알았습니다. 이제 문제는 사람이 일일이 모든 단어를 평가하지 않으면서도 벡터를 만들어낼 수 있는 효과적인 방법을 찾는 것입니다. 이와 관련해서 자연어 처리(Natural Language Processing)에 있어서 혁신적인 아이디어가 2013년에 나왔습니다. 바로 Word2Vec(Word to Vector)입니다.
Word2Vec은 이름 그대로 단어를(특징 또는 의미를 담은) 벡터로 변환하는 방법에 관한 것으로, Google의 Visiting Researcher로 있었던 토마스 미코로브(Tomáš Mikolov, 체코)가 Google의 동료들과 함께 발표한 아주 단순한 구조의 신경망을 기반으로 한 알고리즘입니다.
그렇다면 Word2Vec은 구체적으로 어떤 방법으로 임베딩을 만들어낼까요?
Word2Vec은 언어학적 관점에서 볼 때 영국의 언어학자인 John Rupert Firth가 주창한 "어떤 단어의 의미는 그 단어와 함께 있는 단어들을 통해서 알 수 있다(You shall know a word by the company it keeps)"를 신경망으로 구현한 것입니다. 이는 언어를 습득하는 기본 원리에 대해서 설명한 것인데요. 이것은 우리가 일상생활에서도 늘 경험하는 일입니다. 예를 들면 회사에서 회의 중에 누군가가 사용하는 용어를 처음 들을 때마다 손 들고 그게 무슨 뜻인지 묻는 경우는 많지 않습니다. 대부분은 앞뒤 문맥 혹은 대화의 전체적인 컨텍스트를 보고 그 단어의 의미를 추정합니다. 물론 그렇게 해서 잘못 알게 되거나 여전히 무슨 뜻인지 모르고 넘어가기도 하지만, 몇 번 다른 컨텍스트 속에서 접하게 되면 자연스레 해당 단어에 대해 사전적 정의를 해주지 않아도 의미를 정확히 추정하게 됩니다.
그렇다면 Word2Vec에는 위와 같은 언어 습득의 원리가 어떻게 적용되어 있을까요?
Word2Vec은 신경망 학습에 있어 두 가지 방법을 제시했습니다. 첫 번째는 CBOW(Continuous Bag of Words)이고 또 하나는 Skip-gram이라는 방법입니다.
이중 CBOW 방식은 아래의 예시에 있는 것처럼, 특정 단어를 중심으로 앞뒤에 있는 단어(이 경우는 세 개씩)를 입력으로 하고 중심에 있는 "Stars"를 AI가 알아맞힐 수 있도록 학습합니다. 정확히 표현하면 AI가 주어진 입력 단어에 대해 "Stars"를 출력할 때까지 신경망 내 파라미터 값들을 계속 바꿉니다. 그리고 그 중심 단어는 문장의 처음부터 끝까지 한 단어씩 이동하면서 학습을 반복 진행합니다. 이런 방식으로 많은 문장에 대해 반복해서 결정된 파라미터 값이 임베딩 벡터가 됩니다.
(아래의 '엄청 단순히 설명하는 신경망'을 참조하세요.)
 [그림 5] CBOW 방식
[그림 5] CBOW 방식
반대로, Skip-gram의 경우, 중심 단어를 입력으로 주변에 있는 단어를 출력할 수 있도록 학습하며, 이 역시 중심 단어를 문장 처음부터 시작해서 끝까지 한 단어씩 이동하며 반복합니다.
 [그림 6] Skip-gram 방식
[그림 6] Skip-gram 방식
위와 같은 방식의 학습을 통해 얻은 임베딩 벡터들은 앞서 언급된 바와 같이 같은 문장 속에서 많이 사용되는 단어끼리 유사한 벡터를 갖게 되며 그 중에서 유사한 의미를 갖는 단어들은 다른 단어에 비해 더 가까운 위치에 존재하게 됩니다. (다만, 과일 이름이나 RGB 사례와는 달리 Word2Vec을 통해 산출된 임베딩 벡터 내 각 숫자가 무엇을 의미하는지는 알 수 없습니다.)
그러면 여기서 한 가지 의문이 생길 수 있는데, 그럼 반대어는 어떻게 표현될까요? 얼핏 생각하기엔 유사한 의미를 갖는 단어 벡터들은 서로 비슷한/가까운 벡터 공간 내에 위치해 있으니, 반대어는 그 벡터 공간 내에서 가장 먼 위치인 대칭되는 위치에 있지 않을까 생각할 수 있습니다. 예를 들면, (34, 4, 17)로 표현되는 단어는 임베딩 벡터 공간의 원점을 기준으로 대칭 위치인(-34, -4, -17) 주변에 반대어가 있지 않을까 하는 생각입니다. 하지만, 앞서 설명된 ‘상호 유사한/관련이 있는 의미의 단어는 서로 유사한(가까운) 위치에 존재한다’를 다시 생각해 보면, 어떤 A라는 단어의 반대말도 사실은 A와 관련 있다는 뜻이 되기에 원점을 기준으로 대칭 위치에 반대어가 존재하진 않습니다. 예를 들면, "낮(Day)"의 반대말은 "밤(Night)"입니다. 하지만 이들 단어는 모두 시간 관련 표현이기 때문에 "밤(Night)"을 기준으로 "낮(Day)"은 "저녁(Evening)"이라는 단어보다는 멀리 있겠지만, "줄(Cable)", "아버지(Father)" 등의 단어들처럼 완전히 범주가 다른 단어들보다는 서로 가까이 있게 됩니다. 실제로 아래 파이선 코드를 사용해 테스트를 해봐도 이와 같은 결과를 얻을 수 있습니다.
(참고로 유사도는 1에 가까울수록 두 벡터 간 유사도가 높은 것입니다.)
<표 2> 파이선 프로그램 예제 코드
| 파이선 프로그램 (단어 간 유사도 계산) | 실행 결과 |
|---|---|
|
import gensim.downloader as api model = api.load('word2vec-google-news-300') # 기준 단어와 비교할 단어 리스트 base_word = "night" compare_words = ["day", "evening", "father", "cable"] # 유사도 계산 및 출력 for word in compare_words: similarity = model.similarity(base_word, word) print(f"'{base_word}'와 '{word}'의 유사도: {similarity:.4f}") |
'night'와 'day'의 유사도: 0.5070 'night'와 'evening'의 유사도: 0.8095 'night'와 'father'의 유사도: 0.0875 'night'와 'cable'의 유사도: 0.1072 |
- 위의 파이선 코드는 각 단어를 300차원의 벡터로 임베드해 놓은 구글의 Word2Vec 라이브러리를 사용했습니다.
- 별도의 GPU가 없는 10년 된 제 집의 컴퓨터로(i5, 8G 메모리) 위의 단순한 코드를 실행했는데, 결과가 나오기까지 1분이 넘게 소요됐습니다.
참고로, GPT-3의 경우 여러 모델이 존재하는데 가장 상위 모델이 사용하는 임베딩 벡터는 12,288차원입니다. 물론 임베딩 벡터의 차원을 더 높이면 높일수록 좀 더 정확한 의미를 담을 수 있고 단어 간 미묘한 의미적 차이도 반영(학습)할 수 있습니다. 하지만, 그렇다고 해서 무작정 차원이 크다고 해서 좋은 것은 아닐 수 있습니다. 그만큼 학습 및 학습 후 서비스(Inference) 시에 시스템 속도가 너무 느려지는 문제가 발생할 수 있어 최적의 크기로 사용하는 것이 각 LLM들의 노하우일 것입니다.
엄청 단순히 설명하는 신경망(Word2Vec 관련)
신경망은 크게 3개의 층으로 구성되어 있습니다. (아래 그림 참조) 입력층(Input Layer -노란색), 은닉층(Hidden Layer - 파란색), 출력층(Output Layer - 초록색). 각 층은 뉴런(Neuron)으로 구성되어 있으며 아래 그림 속에서 원으로 표현되어 있습니다. 입력층과 출력층은 각각 입력 데이터가 들어오고, 계산된 결과가 출력되는 층입니다. 은닉층은 신경망 내 복잡한 계산이 이뤄지는 곳으로 은닉층 내 각 뉴런은 활성 함수(Activation Function)라는 비교적 단순한 함수를 담고 있으며 1개 이상의 층으로 구성될 수 있습니다. 각 뉴런 간에는 가중치로 연결되어 있고 은닉 뉴런 안에는 Bias(편향값)가 존재합니다. 그리고 이러한 가중치, 편향을 파라미터라고 부릅니다.
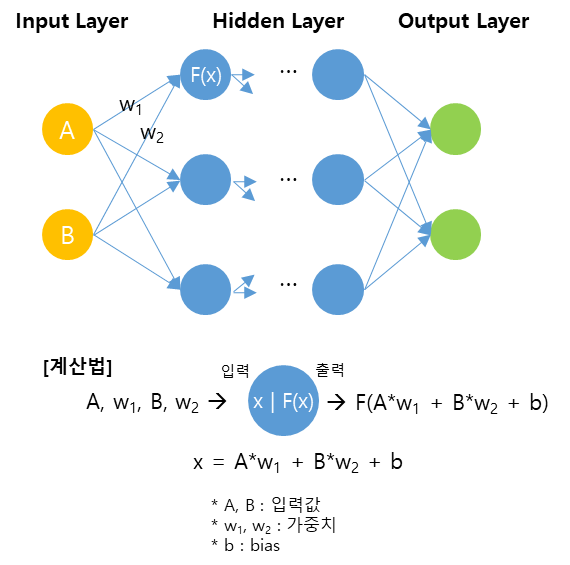 [그림 7] 신경망 구성도
[그림 7] 신경망 구성도
신경망을 사용하려면 먼저 '학습(Training)'이라는 것을 해야 하는데, 여기서 '학습'이라고 하는 것은 이들 뉴런 사이에 있는 파라미터값을 결정/찾아내는 과정으로, 이는 입력값이 은닉층을 거쳐 출력층에 도착했을 때 원하는 결괏값이 나오도록 파라미터값을 변경하는 과정을 의미합니다. (학습 시작 시에는 모든 파라미터는 0 또는 1 같은 임의값이 할당됩니다.)
즉 입력과 출력 사이에 어떠한 '관계'가 존재한다고 할 때, 기존의 일반적인 방법으로는 그 관계를 해석적인 수학 공식으로 만들어낼 수 없거나 혹은 어려울 때 신경망 사용을 시도해 보게 되는데, 신경망도 여전히 해석적인 수학 공식을 만들어내진/찾아내진/도출해 내진 않습니다. 대신에 아주 단순하지만, 많은 수의 활성 함수들과 파라미터값을 튜닝 및 조합하여 원하는 출력값(근삿값)을 만들게 됩니다. 예를 들면, 입력과 출력 간 관계가 사인(Sine) 함수라고 할 때, 이 Sine 함수를 아주 작은 구간의 1차원(y=ax+b) 함수(활성 함수)들을 이리저리 조합해서 Sine 그래프와 비슷하게 만드는 것입니다. 그래서 파라미터 및 활성 함수의 수가 많으면 복잡한 입력과 출력 간의 관계를 정교하게 만들어낼 수 있게 되거나 표현할 수 있게 되어 우리는 이것을 '(인공)지능'이라고 부릅니다. 예를 들어 국어-영어 간 번역을 생각해 보면 분명히 어떤 한국어에 대응하는 영어 표현이 있을 텐데 이것을 IF, THEN 등과 같은 전통적인 로직으로는 규칙을 만들어낼 수 없었지만, LLM이라는 신경망 시스템은 이것을 해낼 수 있게 된 겁니다.
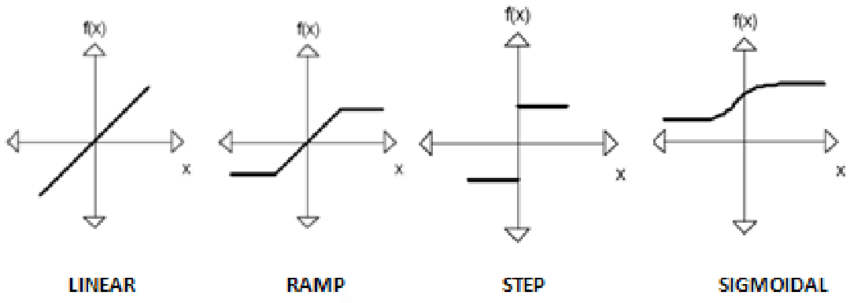 [그림 8] 흔히 사용되는 활성 함수(Activation Function) 예시
[그림 8] 흔히 사용되는 활성 함수(Activation Function) 예시
한편, AI가 특히 학습 단계에서 엄청난 컴퓨팅 파워가 필요한 이유는 일종의 시행착오(Trial-and-Error) 방식처럼 출력층으로 계산되어 나온 출력값과 원래 의도했던 출력값 간 오차를 점차 줄이는 방향으로 수많은 파라미터값을 계속 수정해야 하기 때문입니다. 물론 마구잡이 방식의 시행착오는 아니고 수학적으로 최적화된 방법으로(Gradient Descent) 수정된 파라미터값을 산출하며 오차를 줄여갑니다. 이로 인해 당연히 파라미터의 개수가 많으면 이 작업에 많은 시간이 소요되는데, 예를 들어 1,750억 개의 파라미터를 가진 GPT-3의 경우 학습하는 데 수개월의 시간이 소요됐다고 합니다. (물론 학습 데이터의 양이 많기도 했구요.)
참고로 흔히 Deep Learning이라는 용어의 Deep은 은닉층의 개수가 엄청 많다 혹은 깊다(Deep) 즉 굉장히 복잡한 관계를 모델링/표현할 수 있다는 뜻입니다.
"King" - "Man" + "Woman" = "Queen"
King - Man + Woman = Queen.... 이게 뭘까요? 이 셈식을 처음 보시는 분들은 이게 뭐지 하는 생각을 하실 수 있습니다. 하지만, 이 유명한(?) 셈식은 Word2Vec의 능력을 세상에 알리는 데 많은 기여를 했습니다. 구체적으로 이것의 의미는 "왕"이라는 단어 벡터에서 "남자"라는 단어 벡터를 빼고 "여자"를 더하면 "여왕"이라는 단어의 벡터와 같게 된다는 뜻입니다. (실제 계산은 "King" - "Man" + "Woman" 라는 벡터 연산을 통해 나온 결괏값(벡터)과 전체 임베딩 단어들 중 가장 유사한(가까운 위치) 단어 벡터를 찾으면 "Queen"이 나온다는 의미입니다.) 놀랍지 않나요? "왕"이라는 개념에서 "남자"라는 개념을 빼고 대신에 "여자"라는 개념을 넣으면 "여왕"이라는 개념이 된다는 것을 '계산'할 수 있으니까요. 충분히 많은 양의 문장을 학습하고 나면 추상적인 개념 혹은 의미들을 생각 이상으로 정확하게 인식하고 있음을 알 수 있습니다.
현재 Word2Vec은 위의 예시와 같은 성(性) 관점의 관계도 정확히 표현할 수 있지만, "France" - "Paris' + "Seoul" = "Korea" 같은 연산도 가능합니다.
이처럼 Word2Vec은 놀라운 결과를 보여주며 당시에 획기적인 성과로 받아들여졌습니다. 하지만 Word2Vec 역시 한계가 존재합니다. 가장 큰 문제점은 Word2Vec이 문맥에 따른 단어의 다중 의미를 제대로 표현하지 못한다는 것입니다. 예를 들어 "우리는 다리를 무사히 건너갔다"라는 문장에서 "다리"는 "어제 산에 갔다가 다리를 다쳤다"에서의 "다리"와 다른 의미를 갖지만, Word2Vec에서는 이를 구분하지 못합니다. 좀 더 정확히 표현하면, Word2Vec은 어디까지나 단어를 벡터로 변환하는 기능을 하며, 단어별로 하나의 벡터만을 할당할 수 있어서 같은 단어지만 완전히 다른 의미를 갖는 것을 표현할 수가 없습니다. 대신에, 학습 데이터에 영향을 받긴 하겠지만, 한 단어가 가질 수 있는 여러 의미의 평균 정도 위치로 벡터를 만들어낼 것입니다. 예를 들어 "다리"의 경우라면, 신체 부위로서의 "다리" 벡터와 건축물로서의 "다리" 벡터 중간 정도의 위치로요.
반면에, 이후 4년 뒤에 등장한 Transformer는 단어별 임베딩에서 멈추지 않고, 문장이 입력되면 그 속의 단어들을 임베딩 벡터로 변환한 후 Attention이라는 알고리즘을 통해 입력 문장을 분석하여 문장 속 단어들의 의미를 재해석/조정하는 단계를 거치며 사용자가 원래 의도한 의미를 파악할 수 있습니다.
마치며...
초기 AI에 대한 폭발적 관심에 비해 최근에는 성능은 훨씬 좋아져서 대중화가 되고 있으나, AI에 대한 열기 그 자체는 2023년-2024년에 비하면 줄어들고 있는 것으로 보입니다. 아마도 이젠 일상 업무에서 AI를 접할 수 있는 기회가 늘면서 이 새로운 기술의 장점과 단점 그리고 한계에 대해 경험하고 있기 때문이 아닌가 생각됩니다. (저 역시도 현재의 AI 기술의 한계에 대해 아쉽게 생각합니다.)
하지만, 그럼에도 불구하고 AI 기술은 전 세계적인 관심 속에 엄청난 투자가 지속되고 있는 만큼 발전 속도도 빠릅니다. 그렇기 때문에 지속적인 관심이 필요하다고 봅니다. 앞서 말씀 드린 것처럼 많은 사람들이 ChatGPT가 버전 1.0이 아닌 3.5가 발표될 때까지 그런 기술이 존재하는지도 몰랐습니다. 지속적인 관심을 가지지 않는다면 새로운 변곡점이 또 나타날 때 구경만 하고 있게 될 수 도 있을 것입니다.
▶ 해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에게 저작권이 있습니다.
▶ 해당 콘텐츠는 사전 동의 없이 2차 가공 및 영리적인 이용을 금하고 있습니다.
![]()

삼성SDS 마케팅팀
