머신러닝을 위한 수학과 응용

이번 글에서는 머신러닝에서 사용하는 중요한 수학이론 중 하나인 고유값(Eigenvalue)과 고유벡터(Eigenvector)에 대해 이야기해 보겠습니다. 이는 선형대수(Linear Algebra)에서 가장 중요한 이론 중 하나이며 많은 머신러닝 이론에서 사용되고 있습니다. 고유값과 고유벡터의 이론에 대해 알아본 후 이를 이용하여 데이터의 차원축소 방법인 특이값 분해(Singular Value Decomposition)와 주성분 분석(Principle Component Analysis)에 대해 살펴보겠습니다.
고유값과 고유벡터의 역사
오늘날 선형대수학의 중요한 이론인 고유값과 고유벡터의 개념은 역사적으로 이차형식(Quadratic Forms) 및 미분방정식(Differential Equations) 이론으로부터 발전하였습니다. 18세기에 Leonhard Euler가 강체(Rigid Body)의 회전운동에 대해 연구하면서 주축(Principal Axes)의 중요성에 대해 발견하였습니다. 그리고 Joseph-Louis Lagrange가 이 주축이 관성행렬(Inertia Matrix)의 고유벡터라는 것을 알게 되었습니다. 그리고 Joseph Fourier, Pierre-Simon Laplace, Charles Hermite, Joseph Liouville 등과 같은 유명한 수학자들에 의해 특성방정식(Characteristic Equation)이 개발되고 고유값과 고유벡터의 여러 가지 성질들이 밝혀지게 되었습니다. 전통적으로 이러한 개념은 수학적으로 미분방정식을 풀기 위해 도입되었지만, 최근에는 인공지능을 포함한 머신러닝에서 사용되고 있어 그 중요도가 더 높아졌다고 할 수 있습니다.
고유값과 고유벡터란
정방행렬(Square Matrix)인 선형 변환 A에 의한 변환 결과가 자기자신의 상수배가 되는 0이 아닌 벡터를 고유벡터라 하고 이 상수배 λ의 값을 고유값이라고 합니다. 이를 행렬과 벡터를 사용하여 나타내면 다음 식 (1)과 같습니다.
기하학적으로 고유벡터는 벡터에 선형 변환을 적용할 경우 방향이 변하지 않는 벡터입니다. 그리고 크기만 변화하게 되는데 이때 변화되는 크기가 고유값입니다. 우리는 이러한 벡터와 크기를 찾고 싶어합니다. [그림 1]은 행렬 A에 의해 벡터 x가 방향은 변하지 않은 채 크기만 변화하였음을 볼 수 있습니다. 여기서 x는 A의 고유벡터이며 λ는 고유값입니다.[1]
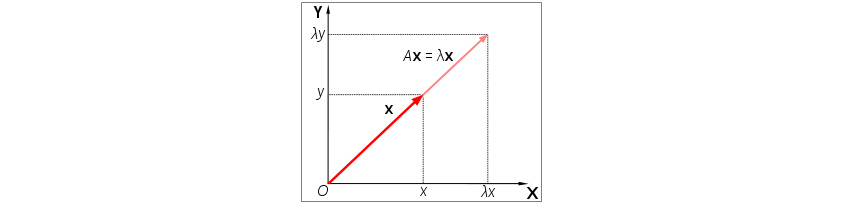 [그림 1] 고유벡터의 변화
[그림 1] 고유벡터의 변화
이제 고유값과 고유벡터를 찾아봅시다. 식 (1)의 우변을 좌변으로 옮겨 변형하면 다음과 같습니다.
여기서 I는 단위행렬(Identity Matrix)입니다. 식 (2)에서 A-λI의 역행렬(Inverse Matrix)이 존재한다고 가정하면 어떻게 될까요? 식 (3)을 보면,
이 되므로 v=0 즉 고유벡터가 항상 0이 되어버립니다. 우리는 0이 아닌 벡터를 찾으려고 하고 이렇게 하기 위해서는 A-λI의 역행렬이 존재하지 않아야 됩니다. 따라서 다음과 같은 조건을 만족시켜야 합니다.
식 (4)를 특성방정식(Characteristic Equation)이라고 합니다. 식 (4)로부터 λ값을 계산할 수 있고 이 값을 고유값이라고 합니다. 고유값을 구한 후 이 값을 식 (2)에 대입하여 고유벡터를 구할 수 있습니다. 고유벡터는 A-λI의 영공간(Null Space)에 있는 벡터이며 유일하지 않고 일반적으로 단위벡터화(‖v‖=1)하여 사용합니다.
아래 [그림 2]는 선형 변환을 보여주고 있으며, 선형 변환 후 붉은색 화살표는 방향이 변화하고 푸른색 화살표는 방향이 변화하지 않고 있습니다. 푸른색 화살표는 고유벡터라고 하며 크기가 변하지 않았기 때문에 고유값은 1이라고 할 수 있습니다. 붉은색 화살표는 방향이 변화하였기 때문에 고유백터가 아닙니다.[1]
 [그림 2] 선형 변환
[그림 2] 선형 변환
대각화와 고유값 분해
n차원 정방행렬 A의 n개의 고유값과 고유벡터를 각각 λ1, ⋯, λn와 v1, ⋯, vn이라고 합니다. 여기서 고유값은 중복이 가능합니다. Q는 각각의 열이 n개의 선형독립적인(Linearly Independent) A의 고유벡터들로 이루어져있는 행렬입니다.
v_1,⋯,v_n은 선형 변환 A의 고유벡터이므로 식 (1)에 의해
입니다. 따라서 식 (6)을 다음과 같이 행렬곱으로 표현할 수 있습니다.
여기서 Λ는 λ1, ⋯, λn를 행렬의 대각선 값으로 갖고 나머지 값은 0인 대각행렬(Diagonal Matrix)입니다. Q는 선형독립적인 n개의 고유벡터로 이루어진 행렬이므로 역행렬이 존재하며, 식 (7)은 다음과 같이 됩니다.
이를 정방행렬 A의 대각화(Diagonalization) 또는 고유값 분해(Eigendecomposition)라고 합니다.
특이값 분해에서의 응용
특이값 분해(Singular Value Decomposition)는 임의의 고유값 분해를 직사각형행렬(Non-square Matrix)에 대해 일반화한 방법으로 데이터의 차원을 축소하는 방법으로 사용되기도 합니다.
여기서 U와 V는 유니터리 행렬(Unitary Matrix)이며, Σ는 대각행렬로 이를 구하는 방법을 살펴보겠습니다. 유니터리 행렬은 다음을 만족하는 행렬입니다.
따라서 다음의 성질도 만족합니다.
[그림 3]은 특이값 분해의 행렬곱을 시각화한 그림입니다.[2]
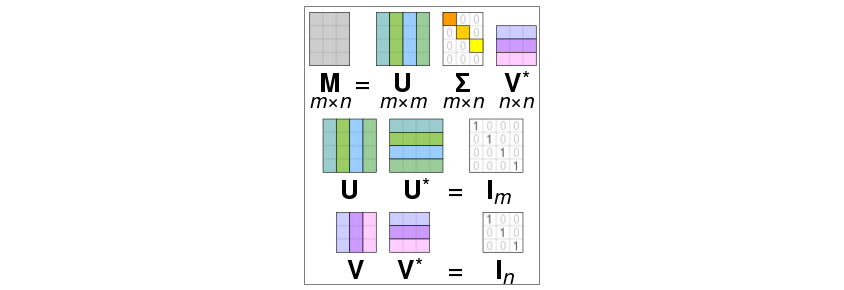 [그림 3] 특이값 분해의 행렬곱
[그림 3] 특이값 분해의 행렬곱
식 (9)와 (11)에 의해서,
= U|Σ|2UT ....................... (13)
식 (13)이 얻어지며 정방행렬의 대각화 식 (8)에 의해 U는 AAT의 고유벡터들로 이루어진 행렬입니다. 마찬가지 방법에 의해
= V|Σ|2VT ......................... (14)
이므로 V는 ATA의 고유벡터들로 이루어진 행렬입니다. 그리고 식 (13) 또는 (14)에 의해 Σ는 AAT또는 ATA의 고유값의 제곱근으로 이루어진 대각행렬입니다.
[그림 4]는 특이값 분해를 2차원 행렬로 시각화한 모습입니다. 위는 M의 작용으로 단위 원이 선형 변환한 모습, 왼쪽은 V의 작용으로 회전한 모습, 오른쪽은 U의 작용으로 다르게 회전한 모습, 아래는 Σ의 작용으로 크기가 변화한 모습을 나타냅니다.[2]
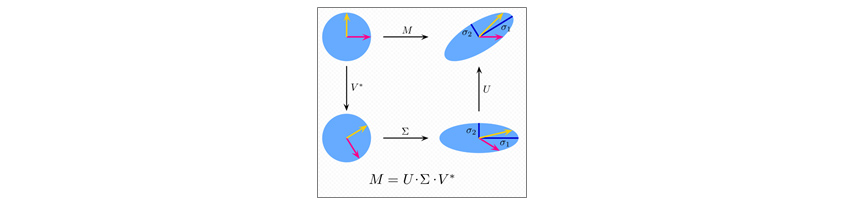 [그림 4] 특이값 분해의 2차원 행렬
[그림 4] 특이값 분해의 2차원 행렬
데이터 차원축소를 위해서는 Truncated SVD라고 하는 방법을 사용하는데 이는 식 (9) 대각행렬 Σ에서 상위 k개의 고유값만 남기고 나머지는 0으로 하여 만들어진 행렬을 가지고 계산을 합니다. 상위 k개의 고유값만 남긴 대각행렬을 Σk라 하고 여기에 대응하는 U와 V의 요소도 제거하고 이를 Uk와 Vk라고 하면 k차원으로 축소된 데이터 Ak는
와 같은 방법으로 얻어집니다.
 [그림 5] Truncated SVD를 이용하여 k 차원으로 축소된 데이터를 계산
[그림 5] Truncated SVD를 이용하여 k 차원으로 축소된 데이터를 계산
주성분 분석에서의 응용
주성분 분석은 1901년 Karl Pearson에 의해 처음 개발되었으며, 고차원의 데이터를 정보의 손실을 최소화하며 저차원의 데이터로 변환시키는 방법입니다. 데이터를 한 개의 축으로 사상시켰을 때 그 분산이 가장 커지는 축을 첫 번째 주성분, 두 번째로 커지는 축을 두 번째 주성분으로 놓이도록 새로운 좌표계로 데이터를 선형 변환하는 것입니다. 원본 데이터를 각 특성(데이터의 각 열을 의미)에 대해 평균을 0으로 만든 데이터를 X라 하면 선형 변환 W를 적용한 새로운 좌표 위의 데이터 T를 찾는 것으로 볼 수 있으며,
이를 위한 W를 찾는 것이 목적입니다. W는 T의 각 특성이 최대의 분산을 갖도록 하는 선형 변환입니다. 이는 데이터의 특성을 가장 잘 설명하기 위해서는 특성들의 분산이 최대화되어야 하기 때문입니다. 이를 위하여 X의 공분산에 대한 고유치와 고유벡터를 이용합니다. 그리고 n개의 특성 중 k개의 주성분을 계산한다고 할 때 고유치가 큰 순위에 해당하는 k개의 고유치를 계산합니다.
그리고 이에 해당하는 고유벡터를 가지고 선형 변환 W를 얻어냅니다.
이 W를 적용하여 얻어진 행렬 T가 특성이 k개인 선형 변환된 데이터입니다.
[그림 6]은 중심점의 좌표가 (1, 3)이고, (0.878, 0.478) 방향으로 3, 이와 수직한 방향으로 1의 표준편차를 가지는 다변량 정규분포에 대한 주성분 분석입니다. 화살표의 길이는 공분산행렬 고유값의 제곱근에 해당하며, 고유벡터의 끝점이 평균점에 위치한 채로 각 주성분의 방향을 나타냅니다.[3]
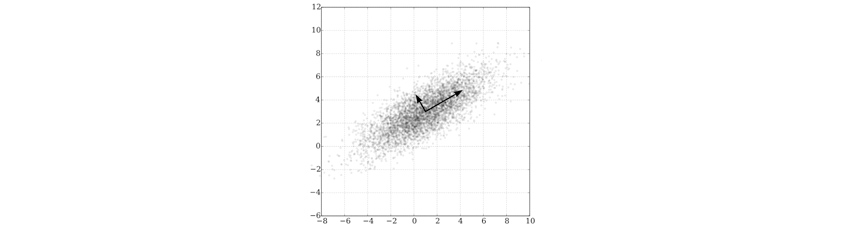 [그림 6] 다변량 정규분포에 대한 주성분 분석
[그림 6] 다변량 정규분포에 대한 주성분 분석# References
[1] https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors
[2] https://en.wikipedia.org/wiki/Singular_value_decomposition
[3] https://en.wikipedia.org/wiki/Principal_component_analysis
[4] https://web.mit.edu/be.400/www/SVD/Singular_Value_Decomposition.htm
▶ 해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에게 저작권이 있습니다.
▶ 해당 콘텐츠는 사전 동의 없이 2차 가공 및 영리적인 이용을 금하고 있습니다.

삼성SDS 분석플랫폼Lab
슈퍼컴퓨터를 이용한 수치해석 분야를 연구하여 박사학위를 취득하였습니다. 이를 응용하여 삼성SDS 분석플랫폼Lab에서 Brightics(삼성SDS AI 빅데이터 플랫폼)의 신기술을 연구개발하고 있습니다.